1 杨氏模量 E
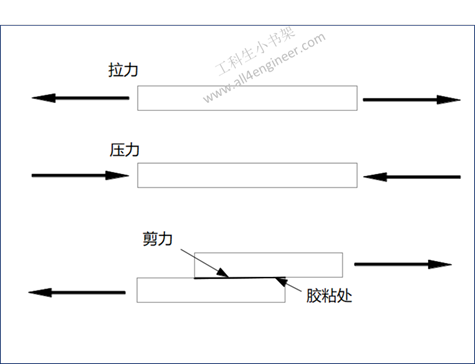
杨氏模量也称杨氏模数(英语:Young’s modulus),一般将杨氏模量习惯称为弹性模量。弹性材料承受正向应力时会产生正向应变,在形变量没有超过对应材料的一定弹性限度时,定义正向应力与正向应变的比值为这种材料的杨氏模量。其公式为:
E = 应力 / 应变
= σ / ε
= (F / A) / (dL / L)
式 1
其中:
- E = 杨氏模量 (Pa, N/m2)
- σ = 应力(N)
- ε =应变(m / m)
- F = 载荷(N)
- dL =物体的伸长或压缩量(m)
- L =物体原始的长度(m)
2 应变-ε
应变是“由于应力导致的固体变形”-尺寸变化除以尺寸的原始值-可以表示为
ε = dL / L
式 2
其中:
- ε =应变(m / m)
- dL =物体(m)的伸长或压缩
- L =物体的长度(m)
只要应力小于材料的屈服强度,就可以用上式来预测物体的伸长或压缩量。
3 应力-σ
应力是每单位面积所受的力,可以表示为:
σ= F / A
式 3
其中:
- σ=应力(N / m2)
- F =施加力(N,lb)
- A =物体的受力面积(m2)
4 常见材料拉伸杨氏模量,抗拉强度和屈服强度。
| 材料 | 拉伸模量
E(GPa) | 极限抗拉强度
σ(MPa) | 屈服强度
σ(MPa) |
| ABS塑料 | 1.4-3.1 | 40 | – |
| 亚克力(丙烯酸塑料) | 3.2 | 70 | – |
| 铝青铜 | 120 | – | – |
| 铝 | 69 | 110 | 95 |
| 铝合金 | 70 | – | – |
| 锑 | 78 | – | – |
| 芳纶 | 70-112 | – | – |
| 铍 | 287 | – | – |
| 铍铜 | 124 | – | – |
| 铋 | 32 | – | – |
| 硼 | – | – | 3100 |
| 黄铜 | 102-125 | 250 | – |
| 海军黄铜 | 100 | – | – |
| 青铜 | 96-120 | – | – |
| 镉 | 32 | – | – |
| 碳纤维增强塑料 | 150 | – | – |
| 碳纳米管,单壁 | 1000 | – | – |
| 铸铁4.5%C,ASTM A-48 | – | 170 | – |
| 纤维素,棉花,木浆和再生 | – | 80-240 | – |
| 醋酸纤维素,模制 | – | Dec-58 | – |
| 醋酸纤维素片 | – | 30-52 | – |
| 硝酸纤维素,赛璐oid | – | 50 | – |
| 氯化聚醚 | 1.1 | 39 | – |
| 氯化PVC(CPVC) | 2.9 | – | – |
| 铬 | 248 | – | – |
| 钴 | 207 | – | – |
| 水泥 | 17 | – | – |
| 铜 | 117 | 220 | 70 |
| 钻石(C) | 1220 | – | – |
| 环氧树脂 | 3 | 26-85 | – |
| 纤维板,中密度 | 4 | – | – |
| 亚麻纤维 | 58 | – | – |
| 玻璃 | 50-90 | 50 | – |
| 玻璃纤维增强聚酯基体 | 17 | – | – |
| 金 | 74 | – | – |
| 花岗岩 | 52 | – | – |
| 石墨烯 | 1000 | – | – |
| 灰铸铁 | 130 | – | – |
| 麻纤维 | 35 | – | – |
| 因科内尔 | 214 | – | – |
| 铱 | 517 | – | – |
| 铁 | 210 | – | – |
| 铅 | 13.8 | – | – |
| 金属镁(Mg) | 45 | – | – |
| 锰 | 159 | – | – |
| 大理石 | – | 15 | – |
| MDF-中密度纤维板 | 4 | – | – |
| 汞 | – | – | – |
| 钼(Mo) | 329 | – | – |
| 蒙乃尔金属 | 179 | – | – |
| 镍 | 170 | – | – |
| 镍银 | 128 | – | – |
| 镍钢 | 200 | – | – |
| 铌(Co) | 103 | – | – |
| 尼龙6 | 2-Apr | 45-90 | 45 |
| 尼龙66 | – | 60-80 | – |
| 橡木(沿纹理) | 11 | – | – |
| 酚醛树脂 | – | 33-59 | – |
| 苯酚甲醛模塑料 | – | 45-52 | – |
| 磷青铜 | 116 | – | – |
| 松木(沿纹理) | 9 | 40 | – |
| 铂 | 147 | – | – |
| 钚 | 97 | – | – |
| 聚丙烯腈,纤维 | – | 200 | – |
| 聚苯并恶唑 | 3.5 | – | – |
| 聚碳酸酯 | 2.6 | 52-62 | – |
| 聚乙烯HDPE(高密度) | 0.8 | 15 | – |
| 聚对苯二甲酸乙二醇酯,PET | 2-2.7 | 55 | – |
| 聚酰胺纤维 | 2.5 | 85 | – |
| 聚异戊二烯,硬橡胶 | – | 39 | – |
| 聚甲基丙烯酸甲酯(PMMA) | 2.4-3.4 | – | – |
| 聚酰亚胺芳烃 | 3.1 | 68 | – |
| 聚丙烯,PP | 1.5-2 | 28-36 | – |
| 聚苯乙烯,PS | 3-3.5 | 30-100 | – |
| 聚乙烯,LDPE(低密度) | 0.11-0.45 | – | – |
| 聚四氟乙烯(PTFE) | 0.4 | – | – |
| 聚氨酯浇铸液 | – | Oct-20 | – |
| 聚氨酯弹性体 | – | 29-55 | – |
| 聚氯乙烯(PVC) | 2.4-4.1 | – | – |
| 钾盐 | – | – | – |
| 铑 | 290 | – | – |
| 橡胶,小应变 | 0.01-0.1 | – | – |
| 蓝宝石 | 435 | – | – |
| 硒 | 58 | – | – |
| 硅 | 130-185 | – | – |
| 碳化硅 | 450 | – | 3440 |
| 银 | 72 | – | – |
| 钠 | – | – | – |
| 钢,高强度合金ASTM A-514 | – | 760 | 690 |
| 精钢AISI 302 | 180 | 860 | 502 |
| 钢,结构ASTM-A36 | 200 | 400 | 250 |
| 钽 | 186 | – | – |
| 钍 | 59 | – | – |
| 锡 | 47 | – | – |
| 钛 | – | – | – |
| 钛合金 | 105-120 | 900 | 730 |
| 牙釉质 | 83 | – | – |
| 钨(W) | 400-410 | – | – |
| 碳化钨(WC) | 450-650 | – | – |
| 铀 | 170 | – | – |
| 钒 | 131 | – | – |
| 铁艺 | 190-210 | – | – |
| 锌锌 | 83 | – | – |
表 1
1 Pa (N/m2) = 1×10-6 N/mm2 = 1.4504×10-4 psi
1 MPa = 106 Pa (N/m2) = 0.145×103 psi (lbf/in2) = 0.145 ksi
1 GPa = 109 N/m2 = 106 N/cm2 = 103 N/mm2 = 0.145×106 psi (lbf/in2)
1 Mpsi = 106 psi = 103 ksi
1 psi (lb/in2) = 0.001 ksi = 144 psf (lbf/ft2) = 6,894.8 Pa (N/m2) = 6.895×10-3 N/mm2