在飞机的飞行原理中,我们介绍了飞行中作用在飞机上的四个基本力:升力,阻力,推力和重力。现在,我们将更仔细地研究两个空气动力升力和阻力,研究两种力之间的关系,研究它们如何相互影响,并学习如何对合力进行无量纲化。我们将特别关注机翼,但是气动载荷背后的概念可以轻松地扩展到飞机的任何其他组件,例如机身,发动机整流罩甚至是机盖。
1.1 压力和剪切载荷
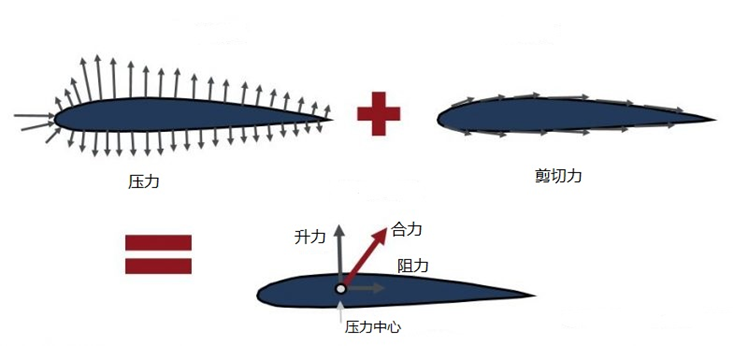
机翼在空气中运动时,压力和剪切载荷分布在整个机翼表面。压力载荷局部垂直于机翼表面。剪切载荷局部平行于机翼表面。
沿表面的每个点取局部压力贡献并将每个贡献累加会产生作用在机翼上的净压力。类似地,沿着机翼表面累加剪切力会得到净剪切力。作用在机翼上的空气动力是压力和剪切力之和,与截面形状无关。
垂直净力称为升力,水平净力称为阻力。净升力和阻力作用在翼型的压力中心。但是,压力中心并不固定,而是随着翼型迎角的变化而变化。常见的方法是使用机翼四分之一弦上指定的点。 这是指从弦线起沿弦线四分之一的点。 将合成的升力和阻力从压力中心移至四分之一弦时,需要增加一个力矩以实现力平衡。 因此,一个俯仰力矩等于升力乘以四分之一弦和压力中心之间的力矩臂,以达到静态平衡(此处我们忽略了剪切力的分量,因为相对于升力该分量对总俯仰力矩的影响可以忽略不计)。
因此,我们可以将翼型上产生的空气动力指定为作用在四分之一弦上的升力和阻力加上平衡的俯仰力矩。
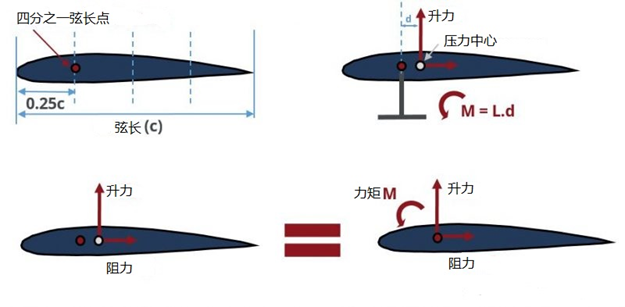
四分之一弦的位置以及对组件产生的空气动力和力矩的解析
1.2 无量纲系数
每个空气动力都取决于以下参数:
F=fn(V∞,ρ,α,μ,a∞)
V∞=自由流速度
ρ=介质密度
α=迎角
μ=介质粘度
a∞=自由流声速
我们可以通过以下方式对力和力矩进行无量纲化:
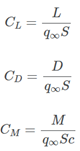
L=升力
D=阻力
M=力矩
S=参考面积 (通常指机翼面积)
q∞=动压
升力,阻力和俯仰力矩的无量纲话,可以用来比较两个不同尺寸,形状和方向的空气动力体,并对结果进行归一化,以解决由物体大小和流体条件产生的力的变化。
1.3 流体相似性
上面列出的无量纲系数不能完全描述力的分量和力矩,因为上面的定义中未包含许多参数。 我们引入了两个流体参数:雷诺数和马赫数,以充分描述流体。
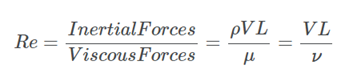
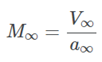
L=物体的特征长度(在航空设计中通常为机翼弦或机身长度)
μ=流体的动态粘度
ν=流体的运动粘度
M∞ =马赫数
V∞=自由流速度 a∞=自由流声速 通常的做法是通过风洞实验,在一系列迎角范围内生成一组空气动力学数据,以了解飞机或车辆在其姿态变化时的表现。但是,一个完整模型的风洞测试非常昂贵,因为风洞的大小和达到典型飞机飞行速度所需的能量是天文数字。 作为替代,工程师们使用上面定义的方程式,可以通过确保真实飞机的雷诺数和马赫数与模型彼此匹配,在比例模型上对动态相似的流体进行建模。 这是非常有力的结论,因为可以通过确保流体相似性,在较小的隧道中按比例对全尺寸飞机的实际响应进行建模。通常很难在单个测试中同时获得匹配的雷诺数和马赫数。 但可以通过对条件进行建模,来得到近似于实际飞行的测试数据。
