1 复合材料单向带杨氏模量计算方法
以航空上常用的单向带预浸料M21/35%/UD268/T700为例:
| 材料 | 模量E (GPa) | 体积含量 (%) | 密度 ρ (g/cm3) |
| 碳纤维-carbon fibre | 235 | 57.2% | 1.78 |
| 基质(树脂)-matrix (resin) | 3.5 | 42.8%(重量比为35%) | 1.28 |
1.1 单向带复合材料模量的计算
复合材料本质上是两种(多种)材料的混合,其模量可以通过基本材料的属性计算得来。
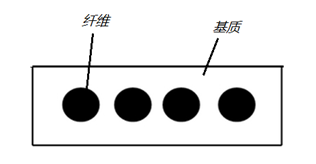
单层(例如预浸料)沿纤维方向杨氏模量的计算:
Ec = EfVf + EmVm
= 235×0.572 + 3.5×0.428
= 136 GPa
- Ec =单层等效模量 (GPa)
- Ef = 纤维的模量 (GPa)
- Vf = 纤维的体积含量(%)
- Em = 基质(树脂)的模量 (GPa)
- Vm = 基质(树脂)的体积含量(%)
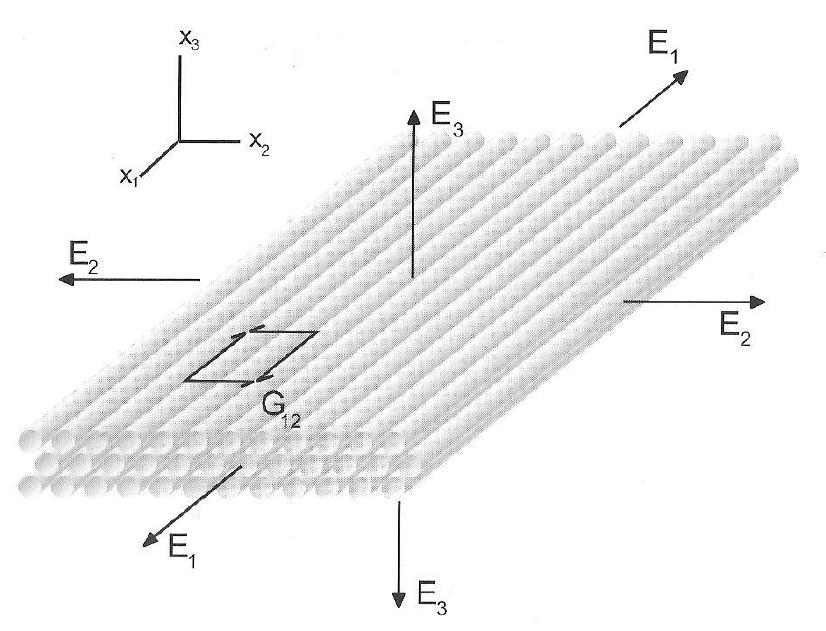
2 复合材料层合板的单层等效模量计算
2.1 纤维角度的效率因子
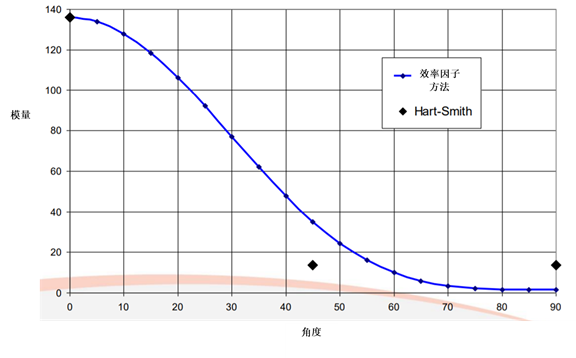
效率因子或克伦切尔因子可用于预测纤维取向对模量的影响,该术语用于根据纤维角度将“混合规则”公式分解为因子:
- an= 纤维百分比
- ? = 纤维角度
- ??= 效率因子
典型的效率因子系数值:
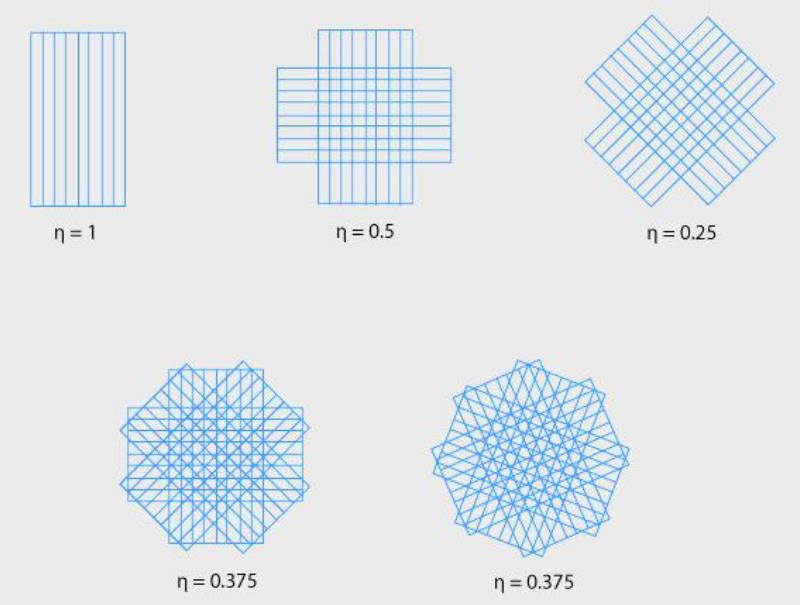
因此对于不同于主纤维方向的单向带的模量可以由下式计算:
E? = ??EfVf + EmVm
因此:
E? = (Cos4? × 235×0.572) + (3.5×0.428)
? = Cos4 ?
- 当纤维0°时,η = 1
- 当纤维45°时,η = 0.25
- 当纤维90°时,η = 0
对于铺层为(0/0/0/+45/-45/0/0/0)的复合材料层合板有:
x方向效率因子:(6/8 × 1) + (2/8 × 0.25) = 0.8125
y方向效率银子:(6/8 × 0) + (2/8 × 0.25) = 0.0625
代入公式:E? = ??EfVf + EmVm
可得:
Ex = (0.8125 × 235×0.572) + (3.5×0.428) = 110.5 GPa
Ey = (0.0625 × 235×0.572) + (3.5×0.428) = 9.9 GPa
2.2 Hart-Smith的百分之十法则
对于常见的仅有四个方向(0、45、90、135或-45)纤维铺层的复合材料,Hart-Smith提出了一个“百分之十法则”,即每45°或90°被认为具有0°方向纤维的十分之一层的刚度和强度。此方法提供了一个简便有效,且足够精确的方法来计算复合材料的刚强度属性。
哈特-史密斯(Hart-Smith)为四轴纤维复合材料结构的初步定型提出了经验性的“百分之十法则”。 在其原始形式下,每层45°或90°的轴向刚度和强度都被认为是参考0°层的十分之一。 认为每个0°或90°层的面内剪切刚度和强度都相当于等效的±45°层的十分之一。
Ex = E11 × (0.1 + 0.9 × % plies at 0°) = 136 × (0.1 + (0.9 × 0.75)) = 136 × (0.775) = 105.4 GPa
Ey = E11 × (0.1 + 0.9 × % plies at 0°) = 136 × (0.1 + (0.9 × 0)) = 136 × (0.1) = 13.6 GPa
2.3 等效模量在效率因子方法和百分之十法则下计算结果的对比