1 拱的分类
最常见的几种拱为固定拱、两铰拱(two-hinged arch)及三铰拱(three-hinged arch)。
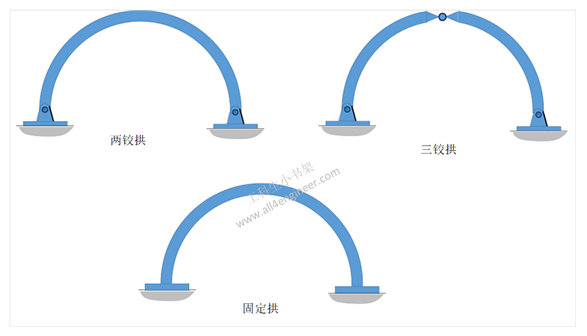
1.1 固定拱
固定拱最常用在跨度较小的钢筋混凝土桥以及隧道。固定拱需承受内部结构因为温度变化产生的热胀冷缩,因此是静不定结构。
1.2 两铰拱
两铰拱(two-hinged arch)最常用在大跨度的桥。这种拱在其拱的底座是由铰支承固定旳,和固定拱的底座不同,铰支承可以旋转,让结构可以形变,以配合因为室外温度变化产生的热胀冷缩。不过仍然会有额外的应力,因此两铰拱仍然是静不定拱,不过情形比固定拱要好很多。
1.3 三铰拱
三铰拱(three-hinged arch)不止在底座有铰支承固定,在其顶点也有铰支承固定。因此可以在水平及垂直的方向变形,以配合因为室外温度变化产生的热胀冷缩。这种拱没有因为热胀冷缩产生的应力,因此是静定结构。三铰拱最常用在中等跨距的拱,例如大型建筑的屋顶。三铰拱的另一个好处是铰支承底座比固定式底座好施工,可以在中等长度范围内使用浅的,轴承型基础。在三铰拱中,拱的热热胀冷缩会让顶点有垂直方向的位移,但二个底座不会有太大的影响,这可以简化底座的设计。
2 均布载荷下的三铰拱计算
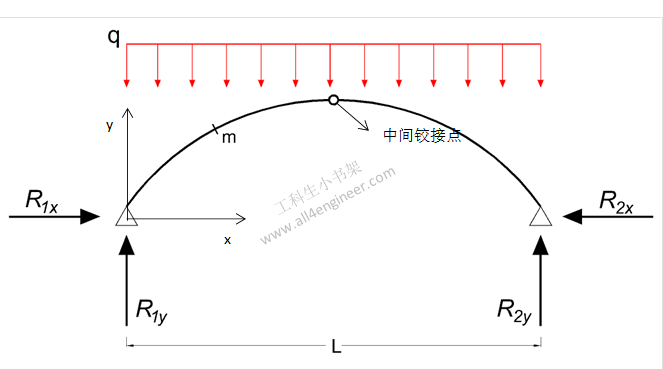
2.1 弯矩计算
Mm = (q L2 / 8) (4 (xm / L – (xm / L)2) – ym / yc)
其中:
- Mm = m点处的弯矩 (Nm)
- q = 均布载荷 (N/m)
- xm = m点的x轴坐标 (m)
- ym = m点的y轴坐标 (m)
- yc = 中间铰接点的y轴坐标(m)
- L = 拱的跨度(m)
2.2 支反力
R1y = R2y
= q L / 2
其中:
- Ry = y向支反力 (N)
R1x = R2x
= q L2 / (8 yc)
其中:
- Rx = x向支反力 (N)
- yc = 中间铰接点的y轴坐标(m)
3 部分均布载荷下的三铰拱计算
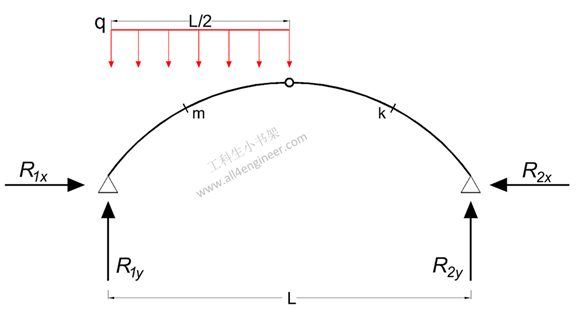
3.1 弯矩计算
Mm = (q L2 / 16) (8 (xm / L – (xm / L)2) – 2 xm / L – ym / yc)
其中:
- Mm = m点处的弯矩 (Nm)
- q = 均布载荷 (N/m)
- xm = m点的x轴坐标 (m)
- ym = m点的y轴坐标 (m)
- yc = 中间铰接点的y轴坐标(m)
- L = 拱的跨度(m)
3.2 支反力计算
R1y = 3 q L / 8
R2y = q L / 8
R1x = R2x= q L2 / (16 yc)
4 点载荷下的三铰拱计算
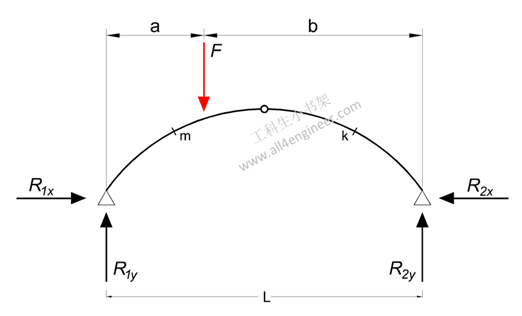
4.1 弯矩计算
Mm = (F a / 2) (2 (b / a) (xm / L) – ym / yc)
Mk = (F a /2) (2 (L – xk) / L – yk / yc)
4.2 支反力
R1y = F b / L
R2y = F a / L
R1x = R2x= F a / (2 yc)
其中:
- Mk = k点处的弯矩 (Nm)
- F = 点载荷 (N)

