计算梁的载荷和支反力,如下图:
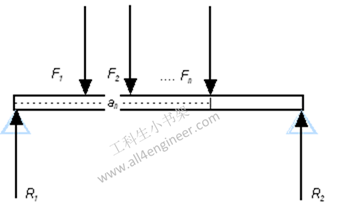
1 力的方程:
F1 + F2 + …. + Fn = R1 + R2
2 力矩的方程:
F1 af1 + F2 af2 + …. + Fn afn = R ar1 + R ar2
- F = 载荷 (N)
- R = 支反力 (N)
- a = 载荷距支点的距离,通常选择其中一个支点为原点 (N)
联立上面2式可得支反力:R1和R2
计算梁的载荷和支反力,如下图:

F1 + F2 + …. + Fn = R1 + R2
F1 af1 + F2 af2 + …. + Fn afn = R ar1 + R ar2
联立上面2式可得支反力:R1和R2
最常见的几种拱为固定拱、两铰拱(two-hinged arch)及三铰拱(three-hinged arch)。
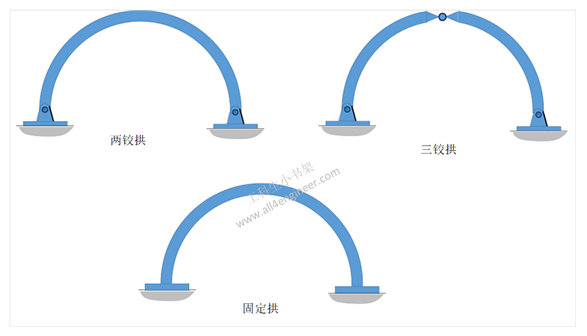
固定拱最常用在跨度较小的钢筋混凝土桥以及隧道。固定拱需承受内部结构因为温度变化产生的热胀冷缩,因此是静不定结构。
两铰拱(two-hinged arch)最常用在大跨度的桥。这种拱在其拱的底座是由铰支承固定旳,和固定拱的底座不同,铰支承可以旋转,让结构可以形变,以配合因为室外温度变化产生的热胀冷缩。不过仍然会有额外的应力,因此两铰拱仍然是静不定拱,不过情形比固定拱要好很多。
三铰拱(three-hinged arch)不止在底座有铰支承固定,在其顶点也有铰支承固定。因此可以在水平及垂直的方向变形,以配合因为室外温度变化产生的热胀冷缩。这种拱没有因为热胀冷缩产生的应力,因此是静定结构。三铰拱最常用在中等跨距的拱,例如大型建筑的屋顶。三铰拱的另一个好处是铰支承底座比固定式底座好施工,可以在中等长度范围内使用浅的,轴承型基础。在三铰拱中,拱的热热胀冷缩会让顶点有垂直方向的位移,但二个底座不会有太大的影响,这可以简化底座的设计。
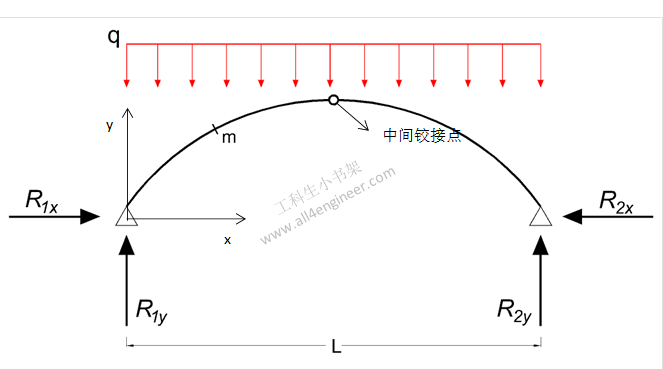
Mm = (q L2 / 8) (4 (xm / L – (xm / L)2) – ym / yc)
其中:
R1y = R2y
= q L / 2
其中:
R1x = R2x
= q L2 / (8 yc)
其中:
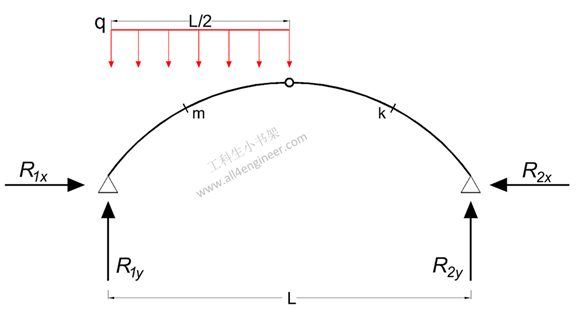
Mm = (q L2 / 16) (8 (xm / L – (xm / L)2) – 2 xm / L – ym / yc)
其中:
R1y = 3 q L / 8
R2y = q L / 8
R1x = R2x= q L2 / (16 yc)
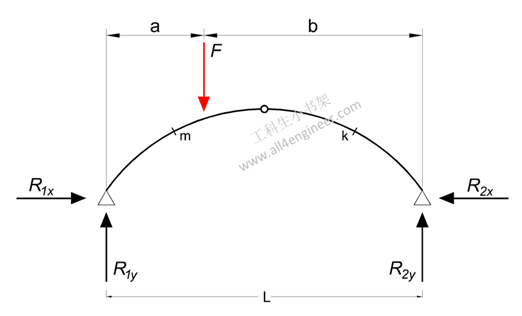
Mm = (F a / 2) (2 (b / a) (xm / L) – ym / yc)
Mk = (F a /2) (2 (L – xk) / L – yk / yc)
R1y = F b / L
R2y = F a / L
R1x = R2x= F a / (2 yc)
其中:
当薄壁管或罐受到内压时,管壁上会产生纵向应力和径向(或环向)应力。
通常认为壁厚小于管道直径的1/20时,认为是薄壁管道,适用于以下计算:
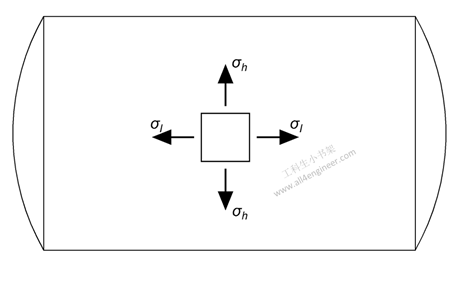
对于两端都封闭的气缸,内部压力会沿着气缸的轴线产生一个力。由该力引起的纵向应力可以计算为
σl = p d / (4 t)
其中:
环向应力沿圆周方向作用,并垂直于圆柱壁的轴线和半径。环向应力可以计算为
σh = p d / (2 t)
其中:
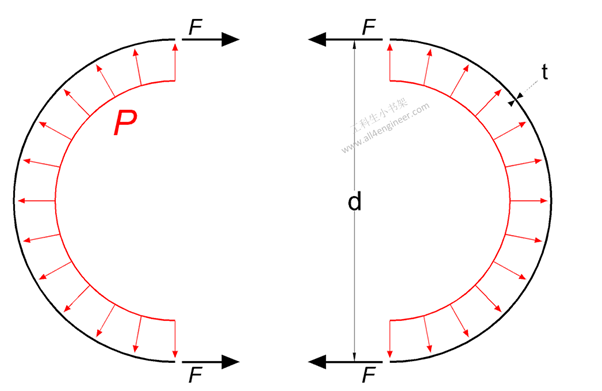
注意:一般碳钢管的最大允许应力低于135 MPa。

当外载荷达到临界载荷F时,柱单元会因屈曲效应而失效。
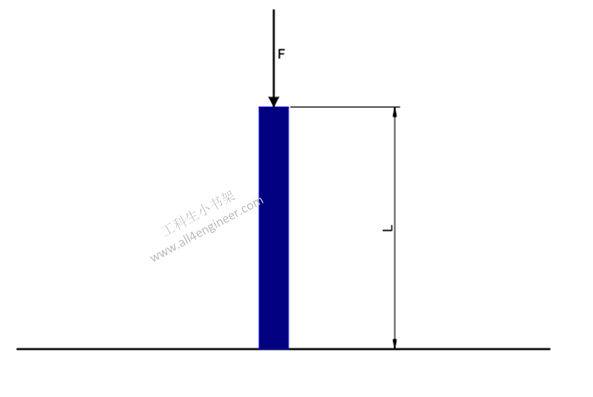
长柱单元可以使用欧拉柱公式进行分析:
F = n π2 E I / L2
式 1
其中:
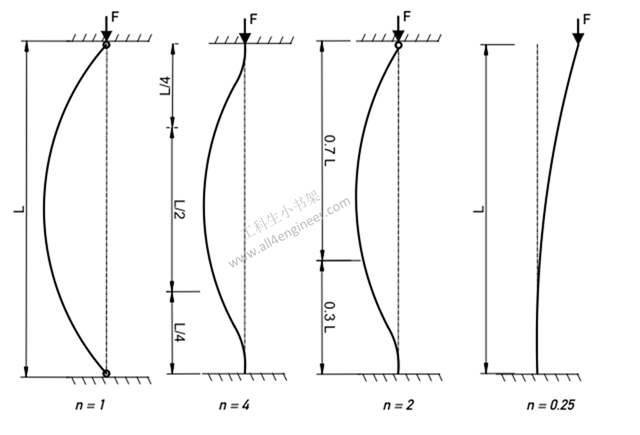
有的时候也用K代替n来描述边界条件:
k = (1 / n)1/2
式 2
K-n 转换表:
| n | 1 | 4 | 2 | 0.25 |
| K | 1 | 0.5 | 0.7 | 2 |
因此最大允许载荷可以表示为:
F = π2 E I / (K L)2
式 3
注意:需要注意的是以上公式为长柱单元的计算方式。
工程上用柱单元的细长比来判断长短性质。
柱单元的有效长度相对于截面积最小回转半径的比例,称为细长比λ(slenderness ratio)
λ=KL/r
式 4
其中:
回转半径r(Radius of Gyration)表示弯曲处距截面质心的距离,在该距离处所有区域都可以集中而对惯性矩没有任何影响。形状相对于每个轴的回转半径由下式给出:
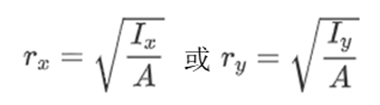
其中:

桁(héng)架(英文:truss)
桁架简单地定义为构件的三角剖分,以形成稳定的结构。三角剖分是数学上的稳定配置。通常桁架具有称为上弦,下弦,垂直弦和对角弦的单元。桁架的主要功能:
在设计过程中有一些基本假设。应该明确的是,桁架的构造应符合设计假设,以避免由于力和载荷的分散而引起的不必要的破坏。以下是桁架设计和计算中的基本假设:
三角形就是最简单的桁架,这类的桁架常出现在屋顶,由二根斜向的椽架及水平的托梁组成一个单元,像在自行车及飞机上也可以看到类似的架构。这类的桁架有形状的稳定性,且已有方法可以分析其各部分的受力,因此由三角形组成的桁架称为简易桁架。像传统由二个相邻三角形组成的钻石型自行车车架,就是简易桁架的例子。
平面桁架位在同一平面上,一般会用数个平面桁架平行排列,组成屋顶及桥梁。
平面桁架的深度,也就是平面桁架上方及下方的上弦杆及下弦杆之间的距离,是桁架之所以成为经济耐用的结构的原因。实心的梁或是梁不论是重量或是成本,都比相同强度的桁架要贵。跨度相同时,若桁架的深度越深,其上弦杆及下弦杆所需的材料越少,但垂直杆及对角线杆需要的材料会增加。因此若深度最佳化,桁架的成本也可以节省。
空间桁架是三维的框架,各杆的末端以旋转接点相接。四面体的外形是最简单的桁架,由六根杆组成,有四个接点。大型的平面结构也可以用四面体组成,在大型的独立输电杆塔中也有用到立体桁架。
四面体桁架

普拉特桁架 普拉特桁架(Pratt truss)是由二位波士顿铁路工程师在1844年申请专利。其设计用垂直杆件来承受压缩力,水平垂直杆件来承受张力,现今这仍是常用的桁架型式,只是原有的木头换成铁,最后再换成钢。普拉特桁架持续受欢迎的原因也许也因为较长的对角杆件只承受因为重力效应产生的张力,因为对角细长杆件若承受压力下,比较容易会挫曲,这在设计上也不易控制。因为若针对固定深度的平面桁架,承受静态、垂直的荷重,普拉特桁架也许是最有效的桁架。
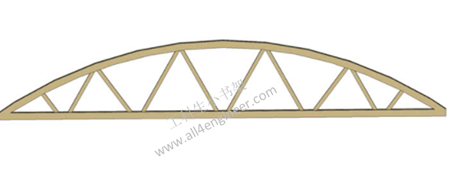
弓弦桁架(Bowstring truss)因其外型得名,最早用在有拱的桁架桥,常和系拱桥混淆。弓弦桁架桥的桥拱和桥面是以杆件相连,而系拱桥是用绳索或钢索连接桥拱和桥面。
在二次大战时时兴建了上千座弓弦桁架,目的是为了飞机库或是其他军用建筑的曲线。连结上弦杆和下弦杆之间的杆有许多不同的变化,从接近等腰三角形到类似普拉特桁架的变体。
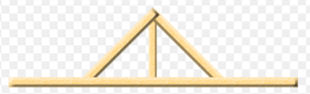
单柱桁架(king post truss)是桁架中最简单的一种,有一个垂直的柱子支撑,两侧则有斜的杆件。

双柱桁架(queen post truss)类似单柱桁架,但中间是二根垂直柱子,之间用梁连接,以提供其结构稳定性,这类桁架只适用在跨距较短的应用中。

透镜桁架桥(Lenticular trusses)是由威廉·道格拉斯在1878年申请专利 ,不过1823年的Gaunless桥是第一座透镜桁架桥,其上弦板及下弦板都是拱形的,因此整体像透镜一样。

美国建筑师 Ithiel Town设计了格构桁架,取代用粗重木头作的桥,他的设计在1820年及1835年申请专利,利用易于处理的木板,对角线的固定在上弦板及下弦板之间。
按外力作用的性质不同,强度主要有屈服强度、抗拉强度、抗压强度、抗弯强度等,工程常用的是屈服强度和抗拉强度,这两个强度指标可通过拉伸试验测出,其单位为Pa。
常用的强度性能指标有拉伸强度和屈服强度(或屈服点)。铸铁、无机材料没有屈服现象,故只用拉伸强度来衡量其强度性能。高分子材料也采用拉伸强度。
承受弯曲载荷、压缩载荷或扭转载荷时则应分别以材料的弯曲强度、压缩强度及剪切强度来表示材料的强度性能。
实验方法:
抗压强度-tensile strength、抗压强度-compression strength、抗剪强度- Shear strength。
抗压、抗拉、抗剪强度的计算式为:
σ=F/A
式 1
其中:
硬度指“固体材料抗拒永久形变的特性”。材料局部抵抗硬物压入其表面的能力称为硬度。固体对外界物体入侵的局部抵抗能力,是比较各种材料软硬的指标。一般硬度越高,耐磨性越好。由于规定了不同的测试方法,所以有不同的硬度标准。
三种主要的硬度定义方式包括:
注意:各种硬度标准的力学含义不同,相互不能直接换算,但可通过试验加以对比。
刚度是指零件在载荷作用下抵抗弹性变形的能力。零件的刚度(或称刚性)常用单位变形所需的了或力矩来表示,刚度的大小取决于零件的几何形状和材料种类(即材料的弹性模量)。刚度要求对于某些弹性变形量超过一定数值后,会影响机器工作质量的零件尤为重要,如机床的主轴、导轨、丝杠等。
工科生小书架为大家总结了20°C条件下常见材料热膨胀系数:
| 材料 | 10-6/K |
| 铝 | 23.2 |
| 纯铝 | 23 |
| 锑 | 10.5 |
| 芳纶 | -4.1 |
| 铍 | 12.3 |
| 水泥 | 6-14 |
| 铅 | 29.3 |
| 镉 | 41 |
| 铬 | 6.2 |
| 钻石 | 1.3 |
| 冰, 0 °C | 51 |
| 铁 | 12.2 |
| 锗 | 6 |
| 玻璃(窗玻璃) | 7.6 |
| 玻璃(工业玻璃) | 4.5 |
| 玻璃(普通) | 7.1 |
| 石英 | 0.5 |
| 金 | 14.2 |
| 花岗岩 | 3 |
| 石墨 | 2 |
| 灰铸铁 | 9 |
| 木头, | 8 |
| 镍钢合金 | 1.7-2.0 |
| 铱 | 6.5 |
| 食盐 | 40 |
| 碳纤维 | ~-0.5 |
| 康铜 | 15.2 |
| 铁镍钴合金 | ~ 5 |
| 铜 | 16.5 |
| 镁 | 26 |
| 锰 | 23 |
| 砖 | 5 |
| 黄铜 | 18.4 |
| 钼 | 5.2 |
| 新银 | 18 |
| 镍 | 13 |
| 铂 | 9 |
| 尼龙 | 120 |
| 聚甲基丙烯酸甲酯(PMMA) | 85 |
| 聚氯乙烯(PVC) | 80 |
| 瓷器 | 3 |
| 银 | 19.5 |
| 锡 | 22 |
| 钢 | 13 |
| 不锈钢 | 14.4-16.0 |
| 钛 | 10.8 |
| 铋 | 14 |
| 钨 | 4.5 |
| 锌 | 36 |
| 硅 | 2.5 |
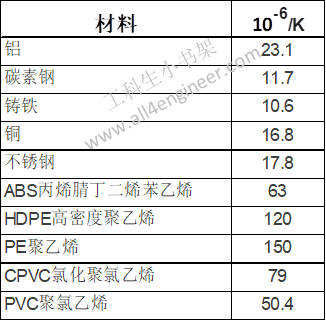
注意:液体和气体的热膨胀系数为体积膨胀
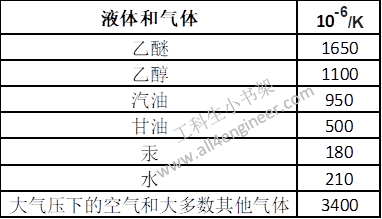
当厚壁管或圆柱体受到内部和外部压力时,壁中会产生轴向,径向,和法向应力。
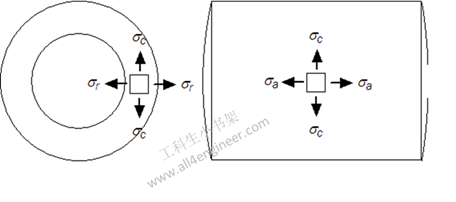
管壁某一点某一点的轴向应力可以表示为:
σa = (pi ri2 – po ro2 )/(ro2 – ri2)
其中:
管壁某一点的圆周方向应力(环向应力)可以表示为:
σc = [(pi ri2 – po ro2) / (ro2 – ri2)] – [ri2 ro2 (po – pi) / (r2 (ro2 – ri2))]
其中:
管壁上某一点的法向应力可以表示为:
σr = [(pi ri2 – po ro2) / (ro2 – ri2)] + [ri2 ro2 (po – pi) / (r2 (ro2 – ri2))]
胡克定律/虎克定律(Hooke’s law),是力学弹性理论中的一条基本定律,内容:固体材料受力后,应力与应变(单位变形量)成线性关系,满足此定律的材料:线弹性/胡克型(Hookean)。从物理的角度看,胡克定律源于多数固体(或孤立分子)内部的原子在无外载作用下处于稳定平衡的状态。
胡克定律应用的一个常见例子是弹簧。在弹性限度内,弹簧的弹力F和弹簧的长度变化量s成线性关系,拉伸或压缩弹簧所需的力可以用胡克定律表示为
F = – k s
在胡克定律的广义变化中,它指出弹性物体或材料的应变/变形与施加于其上的应力成比例。它可以用数学表示为
σ= Eε
其中:
胡克定律仅适用于特定加载条件下的部分材料。钢材在多数工程应用中都可视为线弹性材料,在弹性范围内(即应力低于屈服强度时)胡克定律都适用。另外一些材料(如铝材)则只在弹性范围内的一部分区域行为符合胡克定律。对于这些材料需要定义一个应力线性极限,在应力低于该极限时线性描述带来的误差可以忽略不计。
还有一些材料在任何情况下都不满足胡克定律(如橡胶),这种材料称为“非胡克型”(neo-hookean)材料。橡胶的刚度不仅和应力水平相关,还对温度和加载速率十分敏感。
胡克定律在磅秤制造、应力分析和材料模拟等方面有广泛的应用。
可以将载荷均匀分布的中跨电缆和水平支撑力计算为:
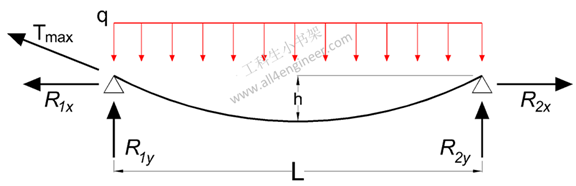
R1x = R2x = Rx = q L2 / (8 h)
式 1
R1y = R2y = Ry = q L / 2
式 2
Tmax = (Rx2 + Ry2)0.5
式 3
电缆的长度S可以近似为:
S = L + 8 h2 / (3 L)
式 4
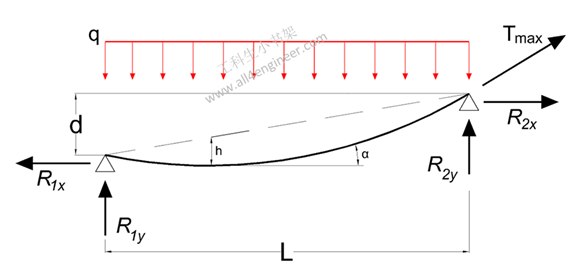
负载均匀分布的水平电缆和支撑力可以计算为:
R1x = R2x = Rx = q L2 / (8 h)
式5
电缆末端的垂直支反力可以计算为:
R1y = R2y = Ry = Rx d / L + q L / 2
式6
作用在支撑端的合力(方向为线缆在支撑处的切线方向)可以计算为:
Tmax = (Rx2 + Ry2)0.5
式7
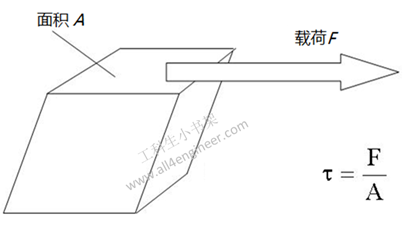
剪力模数(shear modulus)定义为剪应力与剪应变的比值

| 材料 | 剪切模量 – G -(GPa) |
| 铝合金 | 27 |
| 铝,6061-T6 | 24 |
| 铝,2024-T4 | 28 |
| 铍铜 | 48 |
| 黄铜 | 40 |
| 青铜 | 44.8 |
| 镉 | 19 |
| 碳素钢 | 77 |
| 铸铁 | 41 |
| 铬 | 115 |
| 具体 | 21 |
| 铜 | 45 |
| 玻璃 | 26.2 |
| 玻璃,96%二氧化硅 | 19 |
| 镍铬铁合金 | 79 |
| 铁,球墨铸铁 | 63-66 |
| 铁,可锻 | 64 |
| 凯夫拉 | 19 |
| 铅 | 13.1 |
| 镁 | 16.5 |
| 钼 | 118 |
| 蒙乃尔合金 | 66 |
| 镍银 | 48 |
| 镍钢 | 76 |
| 尼龙 | 4.1 |
| 磷青铜 | 41 |
| 胶合板 | 0.62 |
| 聚碳酸酯纤维 | 2.3 |
| 聚乙烯 | 0.12 |
| 橡胶 | 0.0003 |
| 结构钢 | 79.3 |
| 不锈钢 | 77.2 |
| 铸钢 | 78 |
| 钢,冷轧 | 75 |
| 锡 | 18 |
| 钛2级 | 41 |
| 5级钛 | 41 |
| 钛,10%钒 | 42 |
| 钨丝 | 161 |
| 木材,道格拉斯杉木 | 13 |
| 锌锌 | 43 |
| 锌镍 | 76 |
注:
1 GPa = 109 Pa = 0.145 x 106 psi (lbf/in2)
1 x 106 psi = 6.9 GPa
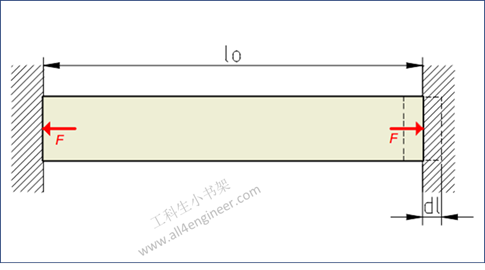
图 1
温度变化引起的线性膨胀可表示为:
dl = α l0 dt
式 1
其中:
若热膨胀无限制将产生的应变或变形可以表示为
ε= dl / l0
式 2
其中:
由此产生的应力可以表示为:
σ = Eε
式 3
其中:
因此两端被限制的圆柱所产生的轴向力可由下式计算:
F = σdt A
= E α dt A
式 4
其中:
图一中圆柱铸铁横截面面积为1000 mm2, 热膨胀系数为12.2×10-6 m/m·K,初始长度l0为300mm,杨氏模量为155GPa,温差为20 °C。
由此产生的轴向力可以计算为:
dl = (12.2×10-12 m/mK) (300 mm) (20 oC)
= 7.32×10-11 m
ε= dl / l0
=(7.32×10-11 m)/ (300mm)
=2.44×10-10
σ= Eε=(155 GPa) · 2.44×10-10=37.8 Pa (N/m2)
F= σdt A =(37.8 Pa)×(1000mm2) = 0.03782 N
刚度是指零件在载荷作用下抵抗弹性变形的能力。
定义为施力与所产生变形量的比值,表示材料或结构抵抗变形的能力。
计算公式为:
K=P/?
式 1
其中:
弹性模量(Modulus)是材料组成的性质;刚度(Stiffness)是结构的性质。即模量是材料的本身的性质;刚度是固体的外延性质,它取决于材料,形状及边界条件。结构刚度在许多工程应用当中非常重要。
对于一个受压或受拉的物体,其轴向刚度为:
K=AE/L
式 2
其中:
对于一个受扭的物体,其扭转刚度为:
K=ML/θ
式 3
其中:
按外力作用的性质不同,强度主要有屈服强度、抗拉强度、抗压强度、抗弯强度等,工程常用的是屈服强度和抗拉强度,这两个强度指标可通过拉伸试验测出,其单位为Pa。
常用的强度性能指标有拉伸强度和屈服强度(或屈服点)。铸铁、无机材料没有屈服现象,故只用拉伸强度来衡量其强度性能。高分子材料也采用拉伸强度。
承受弯曲载荷、压缩载荷或扭转载荷时则应分别以材料的弯曲强度、压缩强度及剪切强度来表示材料的强度性能。
实验方法:
抗压强度-tensile strength、抗压强度-compression strength、抗剪强度- Shear strength。
抗压、抗拉、抗剪强度的计算式为:
σ=F/A
式 1
其中:
金属抗拉强度实验,请参考国标GB/T228或EN ISO6892-1。
注意:测试方法和适用范围按材料、温度等有多个国家标准的规定,须详细查阅相关文献。
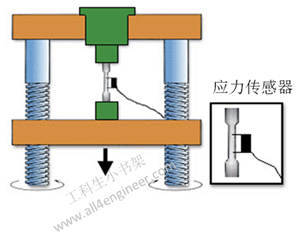
图 1
金属抗压强度实验:请参考国标GB/T7314或 ISO 13314
注意:测试方法和适用范围按材料、温度,压力范围等有多个国家标准的规定,须详细查阅相关文献。
胶粘金属抗剪强度实验:请参考国标G B/T 7 124或ISO 4587
注意:测试方法和适用范围按材料、温度,压力范围等有多个国家标准的规定,须详细查阅相关文献。
材料的抗弯强度,英文:Flexural Strength、Bend Strength,与试件受力情况、截面形状及支撑条件有关。
抗弯强度的计算式为:
σ = (3FL) / (2wd2)
式 2
σ = (FL) / (wd2)
式 3
其中:
一般试验方法是将矩形截面的条形试件放在两支点上,中间加载一个或两个集中荷载:
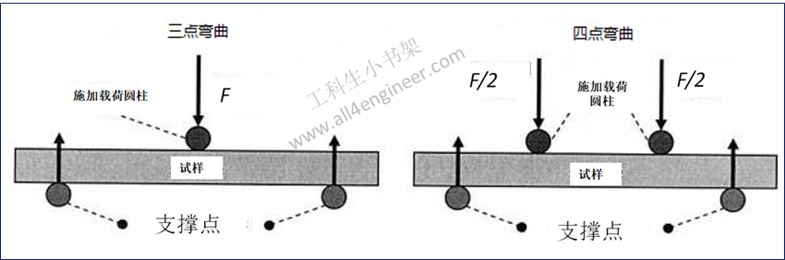
图 2
注:请根据国标- GB/T 6569-86 或ISO 14704-2000查阅具体标准的测试方法及样品要求。测试方法和适用范围按材料、温度、试样类型等有多个国家标准的规定,须详细查阅相关文献。
杨氏模量也称杨氏模数(英语:Young’s modulus),一般将杨氏模量习惯称为弹性模量。弹性材料承受正向应力时会产生正向应变,在形变量没有超过对应材料的一定弹性限度时(符合胡克定律阶段),定义正向应力与正向应变的比值为这种材料的杨氏模量。其公式为:
E = 应力 / 应变
= σ / ε
= (F / A) / (dl / l0)
式 1
其中:
剪力模数(shear modulus)定义为剪应力与剪应变的比值
G = stress / strain
= τ / γ
= (Fp / A) / (s / d)
式 2
其中:
在均质且等向性的材料中:
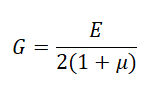
式 3
其中:
体积模量 (Bulk Modulus)也称为不可压缩量,是材料对于表面四周压强产生形变程度的度量。它被定义为产生单位相对体积收缩所需的压强。单位为:Pa(N/m2)
其计算公式为:
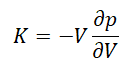
式 4
其中:
体积模量的倒数即为一种物质的压缩率。
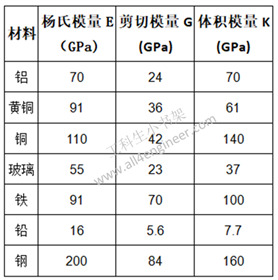
注:1 GPa = 109 Pa (N/m2)
在连续介质力学里,应力定义为单位面积所承受的作用力。分类如下:
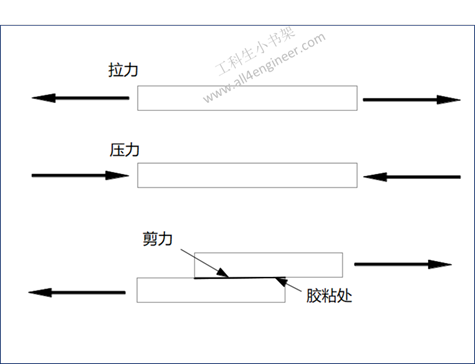
图 1
以上图为例,拉应力和压应力计算公式:
σ = F/A截面
式 1
其中:
10kN的拉力作用在圆形棒直径10mm的杆件上。杆中的应力可以计算为
σ = (10×103N) / (π ((10×10-3 m) / 2)2)
=127388535 (N/m2)
=127 (MPa)
以图1为例,剪应力计算公式:
σ = F/A胶接面
式 2
其中:
剪切力致使物体的两个部分趋于相互滑动的力。
应变的定义:一微小材料元素承受应力时所产生的变形强度(或简称为单位长度变形量),因此是一个无量纲量。
法向应变,可以表示为
ε = dl / lo
= σ / E
式 3
其中:
在已知杆件材料杨氏模量E=200 GPa,施加的应力为σ=127 MPa,杆件初始长度l0=2m,计算杆件的伸长量:
dl = σ lo / E
= (127×106 Pa) (2 m) / (200×109 Pa)
= 0.00127 m
= 1.27 mm
泊松比是指材料在单向受拉或受压时,横向正应变与轴向正应变的绝对值的比值,也叫横向变形系数,它是反映材料横向变形的弹性常数。
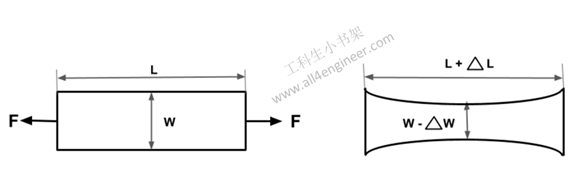
图 1
在材料的弹性范围内加载,泊松比计算为:
µ= |-∆W/W| / |∆L/L|
| 金属名称 | – μ – |
| 铝 | 0.33 |
| 铝青铜 | 0.3 |
| 铍 | 0.024 – 0.03 |
| 铸铁 | 0.26 |
| 青铜 | 0.34 |
| 铜 | 0.36 |
| 金 | 0.42 |
| 铅 | 0.40 – 0.45 |
| 镁 | 0.35 |
| 软钢 | 0.3 |
| 钼 | 0.32 |
| 黄铜 | 0.34 |
| 镍 | 0.31 |
| 磷青铜 | 0.33 |
| 铂 | 0.39 |
| 钚 | 0.15 – 0.21 |
| 银 | 0.37 |
| 不锈钢 | 0.3 |
| 钽 | 0.35 |
| 钍 | 0.27 |
| 锡 | 0.33 |
| 钛 | 0.3 |
| 钨丝 | 0.28 |
| 铀 | 0.21 |
| 铁 | 0.3 |
| 锌 | 0.25 |
重心是指地球对物体中每一微小部分引力的合力作用点。体积,面积或线的“重心”是物体(如果悬吊起来)将达到平衡的点。
浮心是指浮体或潜体水下部分体积的形心。当浮体方位在铅直面内发生偏转时,其水下部分的体积虽保持不变,但其形状却发生变化,因而浮心的位置也相应地移动。
浮心和重心的相对位置对于判断浮体是否为稳定平衡有重要意义。
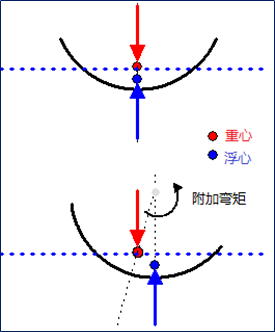
图 1
当船体垂直时,重心和浮力中心在同一垂直线上,船体是稳定态。
对于大多数船体,浮力中心低于重心,并且船体被认为是亚稳定态。
当船体倾斜时,重心保持在与船体相关的相同位置(只要船体没有变化和/或货物没有移动)。 浮力中心将移动以适应新的重心,以适应船体的排水量。
在开始时,重力和浮力将产生一个附加扭矩将船体移回垂直位置。
但如果船体倾斜太多,则浮力中心将移至浮力和重力开始产生作用于相同方向的力矩的位置,那么船体将
倾覆。
质量中心简称质心,指物质系统上被认为质量集中于此的一个假想点。
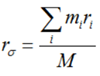
式 1
其中:
若选择不同的坐标系,质心坐标的具体数值就会不同,质心相对于质点系中各质点的相对位置与坐标系的选择无关。质点系的质心仅与各质点的质量大小和分布的相对位置有关
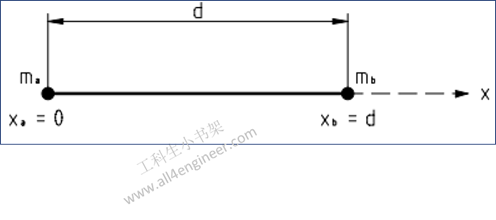
图 1
质心位置计算:
取ma处为坐标原点
Rx = (ma ra + mb rb) / (ma + mb)
= (mb / (ma + mb)) d
式 2
其中:
重心是指地球对物体中每一微小部分引力的合力作用点。体积,面积或线的“重心”是物体(如果悬吊起来)将达到平衡的点。
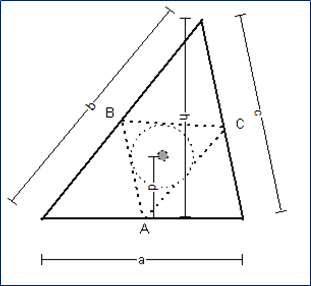
图 1
重心是三角形ABC(三角形边的中点)上刻有圆的中心。
距离d的计算:
d = h(b + c)/ 2(a + b + c)
式 1
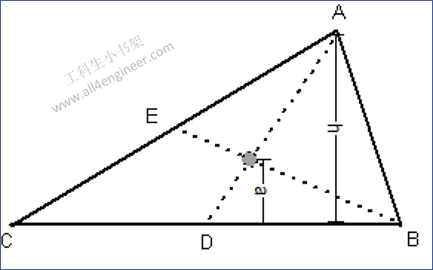
图 2
三角形的重心在直线BE和AD的交点处。
距离a的计算:
a = h / 3
式 2
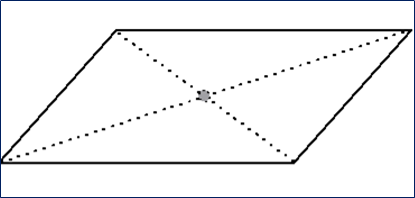
图 3
平行四边形的重心在对角线的交点处。
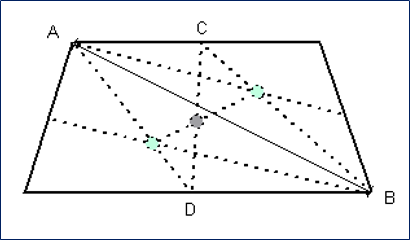
图 4
梯形的重心可以通过将梯形分成两个三角形来估算。重心将在中线CD和三角形重心之间的线的交点处。
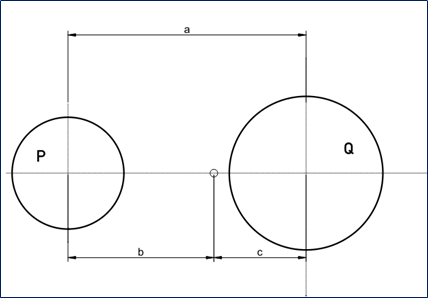
图 5
两个物体的重心用以下公式计算:
b = Q a / (P + Q)
c = P a / (P + Q)
其中:
面惯性矩或面积惯性矩-也称为面积第二矩- I,是一种形状特性,用于预测梁的挠度,弯曲和应力等。
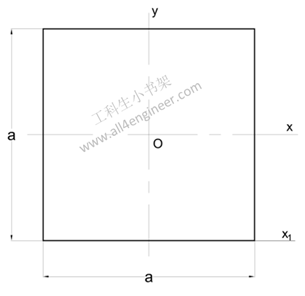
绕轴弯曲的惯性矩的一般公式可以表示为
Ix = ∫ y2 dA
其中:
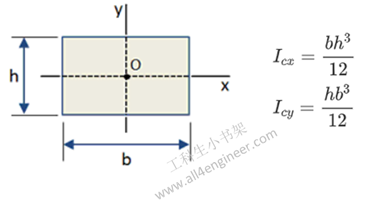
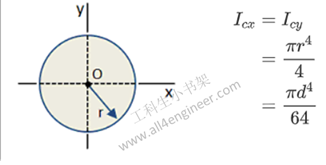

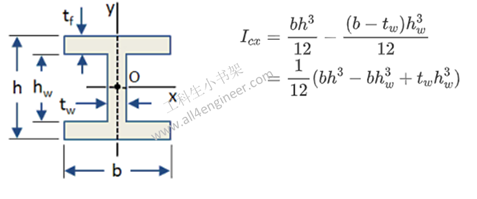
| 单位 | m4 | cm4 | mm4 |
| m4 | 1 | 108 | 1012 |
| cm4 | 10-8 | 1 | 104 |
| mm4 | 10-12 | 10-4 | 1 |
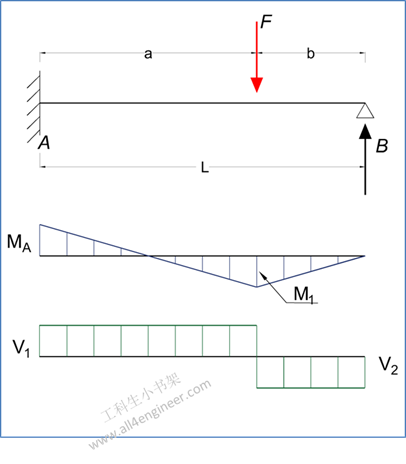
图 1
MA = – F a b (L + b) / (2 L2)
式 1
其中:
MA =固定端A的力矩(Nm)
F = 载荷 (N)
MF = Rb b
其中:
δF = F a3 b2 (3 L + b) / (12 L3 E I)
式 2
其中:
RA = F b (3 L2 – b2) / (2 L3)
式 3
RA =固定端A的支反力(N)
RB = F a2 (b + 2 L ) / (2 L3)
式 4
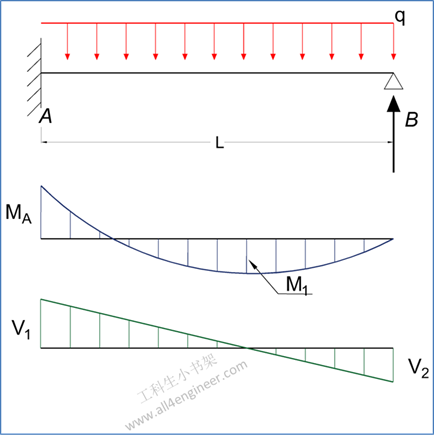
图 2
MA = – q L2 / 8
式 5
其中:
M1 = 9 q L2 / 128
式 6
其中:
δmax = q L4 / (185 E I)
式 7
其中:
δ1/2 = q L4 / (192 E I)
式 8
RA = 5 q L / 8
式 9
RB = 3 q L / 8
式 10
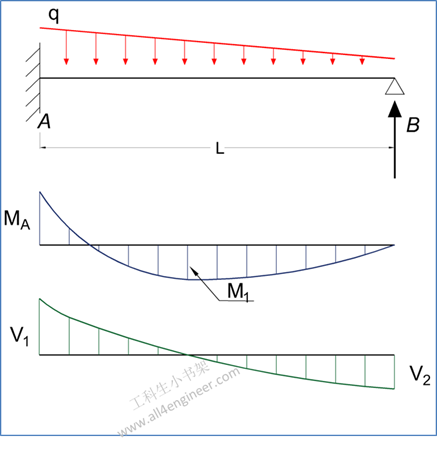
图 3
MA = – q L2 / 15
式 11
其中:
M1 = q L2 / 33.6
式 12
其中:
δmax = q L4 / (419 E I)
式 13
其中:
δ1/2 = q L4 / (427 E I)
式 14
RA = 2 q L / 5
式 15
RB = q L / 10
式 16
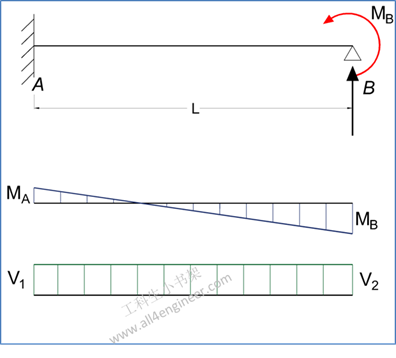
图 4
MA = -MB / 2
式 17
其中:
δmax = MB L2 / (27 E I)
式 18
其中:
RA = 3 MB / (2 L)
式 19
RB = – 3 MB / (2 L)
式 20
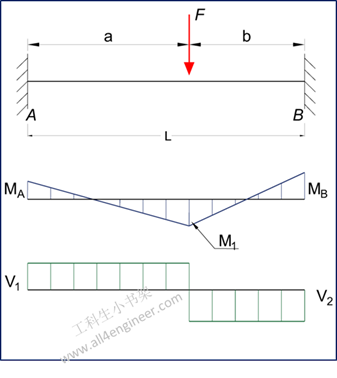
图 1
MA = – F a b2 / L2
式 1
其中:
MB = – F a2 b / L2
式 2
MF = 2 F a2 b2 / L3
式 3
δF = F a3 b3 / (3 L3 E I)
式 4
RA = F (3 a + b) b2 / L3
式 5
RB = F (a + 3 b) a2 / L3
式 6
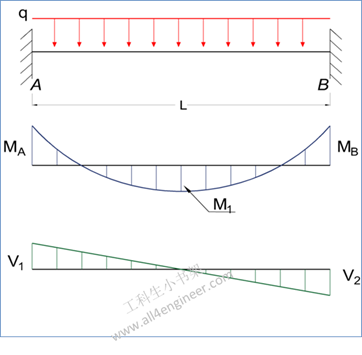
图 2
MA = – q L2 / 20
式 7
MB = – q L2 / 30
式 8
M1 = q L2 / 46.6
式 9
δmax = q L4 / (384 E I)
式 10
RA = RB
= q L / 2
式 11
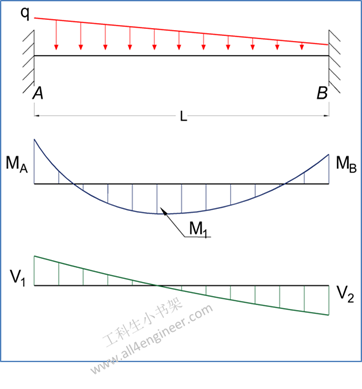
图 3
MA = – q L2 / 20
式 12
MB = – q L2 / 30
式 13
M1 = q L2 / 46.6
式 14
δmax = q L4 / (764 E I)
式 15
δ1/2 = q L4 / (768 E I)
式 16
RA = 7 q L / 20
式 17
RB = 3 q L / 20
式 18
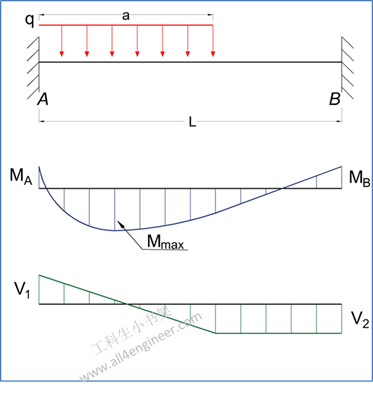
图 4
MA = – (q a2 / 6) (3 – 4 a / l + 1.5 (a / L)2)
式 19
其中:
MB = – (q a2 / 3) (a / L – 0.75 (a / L)2)
式 20
RA = q a (L – 0.5 a) / L – (MA – MB) / L
式 21
其中:
RB = q a2 / (2 L) + (MA – MB) / L
式 22
应力定义:在连续介质力学里,应力定义为单位面积所承受个作用力。
假设受力表面施力方向正交,则叫此应力分量为正应力。
假设受力表面受力方向互相平行,则叫此应力分量为剪应力。
正应力可以表示为:
σ = FN / A
式 1
其中:
剪应力可以表示为:
τ= FV / A
式 2
其中:
10000 N的力作用于10号工字钢 100 x 68 x 4.5,横截面为14.3 cm2。 列中的法向应力可以计算为
σ = (10000 N) / ((14.3 cm2) (0.0001 m2/cm2)
= 6993007 Pa (N/m2)
= 7.0 MPa
屈服强度(材料在从弹性变形转变为塑性变形之前可以承受的应力量)对于钢而言通常为250 MPa。